chapitre 1 suites réelles

télécharger le fichier: chapitre 1 suites réelles (odt)

Chapitre 1: Suites Réelles.

1. Définition élémentaire.

Définition 1

Une suite réelle est une application de

ℕ

dans

ℝ

. L'ensemble des suites réelles se note

ℝ^{ℕ}

Une suite peut se noter

u : n \to u (n)

u = {(u_{n})}_{n \in ℕ}

mais pas

u_{n}

u_{n}

est le n-ième terme de la suite

{(u_{n})}_{n \in ℕ}

u_{n + 1}

est le terme consécutif à

u_{n}

u_{n - 1}

est le terme

antérieur

u_{n}

Une suite peut être définie à partir d'un certain rang.

On distingue les cas où les suites sont définies à partir d'une formule explicite d'avec celles qui sont définies par une relation de récurrence.

Les suites définies à partir d'une formule explicite ont une expression qui permet le calcul immédiat de n'importe quelle valeur du terme de la suite. On note

u_{n} = f (n)

où

f

est une fonction définie sur

[0; + \infty [

Exemple:

\forall n \in ℕ, u_{n} = n^{2} + 2 n + 3

il est aisé de calculer

u_{1000}

En revanche les suites définies par une relation de récurrence nécessite la ou les valeurs de plusieurs termes antérieurs pour calculer la valeur du terme voulu. On note

u_{n + 1} = f (u_{n})

où

f

est définie pour toutes valeurs de

u_{n}

Exemple:

\forall n \in ℕ, u_{n + 1} = u_{n} + n + 3

il n'est pas aisé de calculer

u_{1000}

car on a besoin de

u_{999}

Exemples:

\forall n \in ℕ, u_{n} = n^{2} + 2 n + 3

On a:

u_{0} = 0^{2} + 2 \times 0 + 3 = 3

u_{1} = 1^{2} + 2 \times 1 + 3 = 6

u_{2} = 2^{2} + 2 \times 2 + 3 = 11

\forall n \in ℕ^{*}, u_{n} = \frac{1}{n}

u_{0}

n'existe pas

u_{1} = \frac{1}{1} = 1

u_{2} = \frac{1}{2}

\forall n ⩾ 3, u_{n} = \sqrt{n^{2} - n - 6}

En effet,

\forall n \in ℕ, u_{n} = \sqrt{(n - 3) (n + 2)}

u_{n}

n'existe pas pour des valeurs de

n

strictement inférieures à

3

\forall n \in ℕ, a_{n} = {(- 1)}^{n}

a_{0} = 1

a_{1} = - 1

a_{2} = 1

a_{3} = - 1

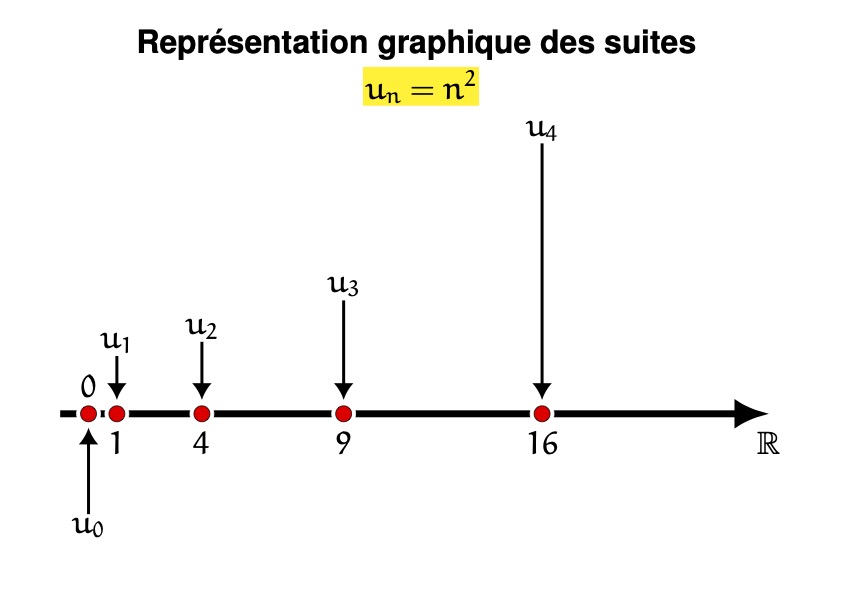
2. Représentation graphique des suites.

On peut représenter graphiquement les suites.

On utilise un axe horizontal qui représente l'ensemble des nombres réels.

On inscrit sur cet axe les valeurs des termes de la suite.

Exemples:

\forall n \in ℕ, u_{n} = \frac{1}{2^{n}}

\forall n \in ℕ, u_{n} = n^{2}

télécharger la figure en braille thermorelief (btm): codex digitalis suite 1 (btm)

télécharger la figure en pdf: codex visualis suite 1 (pdf)

3. Représentation numérique des suites.

En langage Python, pour définir une suite, on peut utiliser le code suivant (ici avec l'exemple

u_{n} = 2 n + 3

)

def suite(n):

return 2*n+3

print(suite(3)) renvoie 9

4. Majorant, minorant.

Définition 2

Soit

(u_{n})

une suite réelle.

(u_{n})

est majorée

\Leftrightarrow \exists M \in ℝ

tel que

\forall n \in ℕ, u_{n} ⩽ M .

Un tel réel

M

s'appelle alors un majorant de la suite

(u_{n})

(u_{n})

est minorée

\Leftrightarrow \exists m \in ℝ

tel que

\forall n \in ℕ, u_{n} ⩾ m .

Un tel réel

m

s'appelle alors un minorant de la suite

(u_{n})

(u_{n})

est bornée si

(u_{n})

est à la fois majorée et minorée.

Exemples:

1) Soit

(u_{n})

définie par

\forall n \in ℕ, u_{n} = \frac{1}{n}

(u_{n})

est majorée par

10

, par

2

, par

1

(u_{n})

est minorée par

- 2

, par

- 1

, par

0

(u_{n})

est bornée.

Soit

(v_{n})

définie par

\forall n \in ℕ, v_{n} = n^{2}

(v_{n})

est minorée par

0

(v_{n})

n'est pas majorée.

3) Soit

(w_{n})

définie par

\forall n \in ℕ, w_{n} = {(- 2)}^{n}

(w_{n})

n'est ni majorée, ni minorée.

5. Sens de variation d'une suite réelle.

Définition 3

Soit

(u_{n})

une suite réelle.

On dit que

(u_{n})

est croissante si

\forall n \in ℕ, u_{n + 1} ⩾ u_{n}

On dit que

(u_{n})

est strictement croissante si

\forall n \in ℕ, u_{n + 1} > u_{n}

On dit que

(u_{n})

est croissante à partir d'un certain rang si

\exists n_{0} \in ℕ

tel que

\forall n > n_{0}, u_{n + 1} > u_{n}

On dit que

(u_{n})

est

dé

croissante si

\forall n \in ℕ, u_{n + 1} ⩽ u_{n}

On dit que

(u_{n})

est strictement

dé

croissante si

\forall n \in ℕ, u_{n + 1} < u_{n}

On dit que

(u_{n})

est

dé

croissante à partir d'un certain rang si

\exists n_{0} \in ℕ

tel que

\forall n > n_{0}, u_{n + 1} < u_{n}

Une suite croissante ou décroissante est dite monotone.

Une suite peut n'être ni croissante ni décroissante.

6. Méthodes pour déterminer le sens de variation d'une suite.

.1. Signe de l'expression

u_{n + 1} - u_{n}

La méthode consiste à étudier le signe de

u_{n + 1} - u_{n}

pour pouvoir ensuite comparer

u_{n}

u_{n + 1}

. On a les résultats suivants:

u_{n + 1} - u_{n} ⩾ 0

, alors la suite

(u_{n})

est croi

ante.

u_{n + 1} - u_{n} ⩽ 0

, alors la suite

(u_{n})

est

dé

croi

ante.

Exemples:

1) Soit

(u_{n})

la suite définie

par

\forall \in ℕ, u_{n} = n^{2}

La suite

(u_{n})

est croissante.

En effet,

\forall n \in ℕ,

u_{n + 1} - u_{n} = {(n + 1)}^{2} - n = n^{2} + 2 n + 1 - n^{2} = 2 n + 1 > 0

2) Soit

(v_{n})

la suite définie par

\forall \in ℕ^{*}, v_{n} = \frac{1}{n}

La suite

(v_{n})

est décroissante.

En effet,

\forall n \in ℕ^{*},

v_{n + 1} - v_{n} = \frac{1}{n + 1} - \frac{1}{n}

= \frac{n}{n (n + 1)} - \frac{n + 1}{n (n + 1)}

= \frac{n - (n + 1)}{n (n + 1)}

= \frac{- 1}{n (n + 1)} < 0

3) Soit

(w_{n})

la suite définie par

\forall \in ℕ, w_{n} = \sqrt{n}

La suite

(w_{n})

est croissante.

En effet,

\forall n \in ℕ,

w_{n + 1} - w_{n} = \sqrt{n + 1} - \sqrt{n}

= (\sqrt{n + 1} - \sqrt{n}) \frac{(\sqrt{n + 1} + \sqrt{n})}{\sqrt{n + 1} + \sqrt{n}}

= \frac{(n + 1) - n}{\sqrt{n + 1} + \sqrt{n}}

= \frac{1}{\sqrt{n + 1} + \sqrt{n}} > 0

Comparaison

de l'expression

\frac{u_{n + 1}}{u_{n}}

avec 1.

La méthode consiste à comparer le rapport

\frac{u_{n + 1}}{u_{n}}

avec

1

, à

la condition que

(u_{n})

ne s'annule pas pour des valeurs de

n

\frac{u_{n + 1}}{u_{n}} ⩾ 1

, alors la suite

(u_{n})

est croi

ante.

\frac{u_{n + 1}}{u_{n}} ⩽ 1

, alors la suite

(u_{n})

est

dé

croi

ante.

Exemples:

1) Soit

(u_{n})

la suite définie par

\forall \in ℕ, u_{n} = n!

La suite

(u_{n})

est croissante.

En effet,

\forall n \in ℕ,

\frac{u_{n + 1}}{u_{n}} = \frac{n + 1!}{n!}

= \frac{(n + 1) \times n \times (n - 1) \times \dots \times 1}{n \times (n - 1) \times \dots \times 1}

= n + 1 ⩾ 1

2) Soit

(v_{n})

la suite définie par

\forall \in ℕ, v_{n} = 2^{- n} = \frac{1}{2^{n}}

La suite

(v_{n})

est décroissante.

En effet,

\forall n \in ℕ,

\frac{v_{n + 1}}{v_{n}} = \frac{2^{- (n + 1)}}{2^{- n}}

= 2^{- n - 1 - (- n)}

= 2^{- n - 1 + n} = 2^{- 1} = \frac{1}{2} < 1

7. Suites particulières.

7.1 Suites arithmétiques.

Définition 4

Soit

(u_{n})

une suite réelle.

La suite

(u_{n})

est arithmétique si et seulement si

\exists r \in ℝ

tel que

\forall n \in ℕ, u_{n + 1} = u_{n} + r

(u_{n})

est arithmétique, le réel

r

est la raison de la suite.

Remarque: si

(u_{n})

est une suite arithmétique, alors nécessairement

r = u_{1} - u_{0}

Théorème 1

Soit

(u_{n})

une suite arithmétique de raison

r

\forall n \in ℕ, u_{n} = u_{0} + nr

\forall (n, p) \in ℕ^{2}, u_{n} = u_{p} + (n - p) r

Exemple:

Soit

(u_{n})

une suite définie par

\forall n \in ℕ, u_{n + 1} = u_{n} - 5, u_{0} = 2

(u_{n})

est une suite arithmétique de raison

r = - 5

u_{1} = 2 - 5 = - 3

u_{2} = - 3 - 5 = - 8

\forall n \in ℕ, u_{n} = 2 - 5 n

7.2 Suites géométriques.

Définition 5

Soit

(u_{n})

une suite réelle.

La suite

(u_{n})

est géométrique si et seulement si

\exists q \in ℝ

tel que

\forall n \in ℕ, u_{n + 1} = {qu}_{n}

(u_{n})

est géométrique et si

u_{0} \neq 0

le réel

q

s'appelle la raison de la suite.

Remarque: si

(u_{n})

est une suite géométrique et si

u_{0} \neq 0

, alors

q = \frac{u_{1}}{u_{0}}

Théorème 2

Soit

(u_{n})

une suite géométrique de raison

q

\forall n \in ℕ, u_{n} = u_{0} \times q^{n}

2) si

q \neq 0

\forall (n, p) \in ℕ^{2}, u_{n} = u_{pq}^{n - p}

Exemple:

Soit

(u_{n})

une suite

définie par

\forall n \in ℕ, u_{n + 1} = 0,7 u_{n}, u_{0} = 2

(u_{n})

est une suite géométrique de raison

q = 0,7

u_{1} = 1,4

u_{2} = 0,98

\forall n \in ℕ, u_{n} = 2 {(0,7)}^{n}

7.3 Suites arithmético-géométriques.

Définition 6

Soit

(u_{n})

une suite réelle.

La suite

(u_{n})

est arithmético-géométrique

si et seulement si

\exists (a, b) \in ℝ^{2}

tels que

\forall n \in ℕ, u_{n + 1} = a u_{n} + b

Exemple:

Soit

(u_{n})

une suite

définie par

\forall n \in ℕ, u_{n + 1} = 0,7 u_{n} - 5, u_{0} = 2

(u_{n})

est une suite arithmético-géométrique.

u_{1} = 0,7 \times 2 - 5 = - 3,6

u_{2} = 0,7 \times (- 3,6) - 5 = - 7,52

7.4 Code Python pour déterminer le n-ième terme d'une suite arithmético-géométrique.

On considère une suite

(u_{n})

définie par

\forall n \in ℕ, u_{n + 1} = a u_{n} + b

où

a

b

sont deux réels fixés. On pose

u_{0} = u 0

informatiquement.

def suite_ag(n):

m=0 #on crée une variable m

u=u0 #on itinitalise la suite u

while m<n:

u=a*u+b

m=m+1

return u

La compilation de ce code renvoie un message d'erreur car les variables u0, a et b ne sont pas déclarées. Il s'agit de l'adapter aux diverses situations rencontrées.

7.5 Code pour afficher les valeurs des termes d'une suite arithmético-géométrique sur un tableur type Excel.

On considère une suite

(u_{n})

définie par

\forall n \in ℕ, u_{n + 1} = k u_{n} + p

où

k

p

sont deux réels fixés. On pose

u_{0} = u 0

informatiquement.

Colonne A: a0=0, a1=a0+1, puis on étend la formule de a1 vers le bas

Colonne B: b0=u0, b1=k*b0+p, puis on étend la formule de b1 vers le bas

8. Convergence des suites.

8.1 Suites convergentes.

Définition 7

Soit

(u_{n})

une suite réelle et soit

γ

un nombre réel.

La suite

(u_{n})

converge vers le nombre

γ

si et seulement si

\forall ϵ > 0, \exists n_{0} \in ℕ, \forall n \in ℕ, (n ⩾ n_{0} \Rightarrow | u_{n} - γ | ⩽ ϵ)

2) Soit

(u_{n})

une suite réelle.

La suite

(u_{n})

est convergente si et seulement si il existe un nombre réel

γ

tel que la suite

(u_{n})

converge vers le nombre

γ

. Dans le cas contraire on dit que la suite est divergente.

Si une suite converge, on écrira

\lim_{n \to + \infty} u_{n} = γ

n

est une variable muette dans cette écriture, ou pourrait donc aussi écrire

\lim_{p \to + \infty} u_{p} = + \infty

Exemples:

\lim_{n \to + \infty} \frac{1}{n} = 0

\lim_{n \to + \infty} \frac{1}{n + 1} = 0

\lim_{n \to + \infty} \frac{n + 1}{n} = \lim_{n \to + \infty} 1 + \frac{1}{n} = 1

CODEX CONVERGENCE 1

Théorème 3

Soit

(u_{n})

une suite réelle.

Si la suite (u_n) converge vers le nombre réel %gamma alors %gamma est unique.

Théorème 4

Soit

(u_{n})

une suite réelle.

Si la suite

(u_{n})

est convergente alors la suite

(u_{n})

est bornée.

8.2 Suites réelles de limite infinie.

Définition 8

Soit

(u_{n})

une suite réelle.

On dit que

(u_{n})

tend vers

+ \infty

quand

n

tend vers

+ \infty

et on écrit

\lim_{n \to + \infty} u_{n} = + \infty

si et seulement si

\forall A \in ℝ, \exists n_{0} \in ℕ, \forall n > n_{0}, (n ⩾ n_{0} \Rightarrow u_{n} ⩾ A)

On dit que

(u_{n})

tend vers

- \infty

quand

n

tend vers

+ \infty

et on écrit

\lim_{n \to + \infty} u_{n} = - \infty

si et seulement si

\forall B \in ℝ, \exists n_{0} \in ℕ, \forall n > n_{0}, (n ⩾ n_{0} \Rightarrow u_{n} ⩽ B)

Remarque: Il est clair qu'une suite réelle de limite infinie n'est pas bornée et est en particulier divergente.

CODEX SUITE + INFINIE

Exemples:

\lim_{n \to + \infty} n = + \infty

\lim_{n \to + \infty} - n = - \infty

8.3 Limites de référence.

Théorème 5

Soit

q \in ℝ

)

- 1 < q < 1

, alors

\lim_{n \to + \infty} q^{n} = 0

) Si

q > 1

, alors

\lim_{n \to + \infty} q^{n} = + \infty

3) Si

q = 1

, alors

\lim_{n \to + \infty} q^{n} = 1

) Si

q ⩽ - 1

, alors

(u_{n})

diverge.

Théorème 6

Soit

α \in ℝ

1) Si

α < 0

alors

\lim_{n \to + \infty} n^{α} = 0

2) Si

α = 0

alors

\lim_{n \to + \infty} n^{α} = 1

3) Si

α > 0

alors

\lim_{n \to + \infty} n^{α} = + \infty

Exemples:

\lim_{n \to + \infty} {0,99}^{n} = 0

\lim_{n \to + \infty} 2^{n} = + \infty

\lim_{n \to + \infty} n^{2} = + \infty

8.4 Opérations sur les limites.

Théorème 7

Soient

(u_{n})

(v_{n})

deux suites convergentes vers

γ

γ'

respectivement, et

(λ, μ) \in ℝ^{2}

La suite

(λ u_{n} + μ v_{n})

converge vers

(λ γ + μ γ')

Théorème 8

Soit

(u_{n})

une suite qui tend vers

+ \infty

. Soit

λ

un réel.

Alors:

\lim_{n \to + \infty} λ u_{n} = + \infty

λ > 0

\lim_{n \to + \infty} λ u_{n} = - \infty

λ < 0

\lim_{n \to + \infty} λ u_{n} = 0

λ = 0

Théorème 9

Soient

(u_{n})

(v_{n})

deux suites convergentes vers

γ

γ'

respectivement.

La suite

(u_{n} \times v_{n})

tend vers

γ \times γ'

Théorème 10

Soient

(u_{n})

(v_{n})

deux suites.

1) Si

(u_{n})

converge vers

γ

(v_{n})

une suite qui tend vers

+ \infty

Alors:

)

\lim_{n \to + \infty} u_{n} v_{n} = + \infty

γ > 0

)

\lim_{n \to + \infty} u_{n} v_{n} = - \infty

γ < 0

2) Si

\lim_{n \to + \infty} u_{n} = + \infty

\lim_{n \to + \infty} v_{n} = + \infty

alors

\lim_{n \to + \infty} u_{n} v_{n} = + \infty

3) Si

\lim_{n \to + \infty} u_{n} = + \infty

\lim_{n \to + \infty} v_{n} = - \infty

alors

\lim_{n \to + \infty} u_{n} v_{n} = - \infty

4) Si

\lim_{n \to + \infty} u_{n} = - \infty

\lim_{n \to + \infty} v_{n} = - \infty

alors

\lim_{n \to + \infty} u_{n} v_{n} = + \infty

Théorème 11

Soient

(u_{n})

(v_{n})

deux suites convergentes vers

γ

γ'

respectivement,

avec

γ'

non nul.

La suite

(\frac{u_{n}}{v_{n}})

tend vers

\frac{γ}{γ'}

Théorème 12

Soit

(u_{n})

une suite réelle.

1) Si

\lim_{n \to + \infty} u_{n} = 0

(u_{n})

strictement positive à partir d'un certain rang, alors

\lim_{n \to + \infty} \frac{1}{u_{n}} = + \infty

2) Si

\lim_{n \to + \infty} u_{n} = 0

(u_{n})

strictement négative à partir d'un certain rang, alors

\lim_{n \to + \infty} \frac{1}{u_{n}} = - \infty

Théorème 13

Soit

(u_{n})

une suite réelle.

\lim_{n \to + \infty} u_{n} = \pm \infty

, alors

\lim_{n \to + \infty} \frac{1}{u_{n}} = 0

On peut résumer les théorèmes 12 et 13 par l'écriture abusive:

\frac{1}{0} = + \infty

\frac{1}{\infty} = 0

On retiendra les 4 formes indéterminées qui ne figurent pas dans les opérations concernant les limites:

(+ \infty) - (+ \infty)

\frac{\infty}{\infty}

\frac{0}{0}

\pm \infty \times 0

Lorsqu'on veut déterminer des limites de suites (et plus tard des limites de fonctions), on veillera à lever les indéterminations si il y en a.

Une méthode consiste à mettre le terme prépondérant en facteur.

On peut aussi utiliser la quantité conjuguée lorsqu'il y a des racines carrés.

Exemples:

\lim_{n \to + \infty} 2 n^{2} + 3 n + 1 = + \infty

Ici, il n'y a pas d'indétermination, on peut raisonner par sommation.

2) Soit

(u_{n})

la suite définie par

\forall n \in ℕ, u_{n} = n^{2} - n - 1

Si on procède par sommation, on obtiendra une limite du type "

\infty - \infty

" qui est indéterminée.

On met le terme prépondérant en facteur dans l'expression de la suite afin d'obtenir un produit.

On obtient

n^{2} (1 - \frac{n}{n^{2}} - \frac{1}{n^{2}}) = n^{2} (1 - \frac{1}{n} - \frac{1}{n^{2}})

Cette expression existe car ici

n

ne sera pas égal à

0

, on s'intéresse au comportement de la suite pour des

valeurs de

n

très grand

Enfin, on fait tendre

n

vers

+ \infty

dans cette expression qui est un produit.

D'une part nous avons

\lim_{n \to + \infty} n^{2} = + \infty

D'autre part

\lim_{n \to + \infty} 1 - \frac{1}{n} - \frac{1}{n^{2}} = 1 - 0 - 0 = 1

Donc

\lim_{n \to + \infty} n^{2} (1 - \frac{1}{n} - \frac{1}{n^{2}}) = + \infty \times 1 = + \infty

3) Soit

(u_{n})

la suite définie par

\forall n \in ℕ, u_{n} = \frac{2 n + 1}{3 n - 4}

Ici, la limite est du type "

\frac{\infty}{\infty}

" qui est indéterminée.

De même que dans le cas précédent, on met le terme prépondérant en facteur au numérateur et au dénominateur.

\frac{2 n + 1}{3 n - 4} = \frac{n (2 + \frac{1}{n})}{n (3 - \frac{4}{n})} = \frac{2 + \frac{1}{n}}{3 - \frac{4}{n}}

\lim_{n \to + \infty} \frac{2 + \frac{1}{n}}{3 - \frac{4}{n}} = \frac{2 + 0}{3 - 0} = \frac{2}{3}

3) La suite définie par

\forall \in ℕ, u_{n} = \sqrt{n + 1} - \sqrt{n}

a une limite du type "

\infty - \infty

On multiplie par la quantité conjuguée, en veillant au fait qu'elle ne s'annule pas pour des valeurs de

n

\forall n \in ℕ,

(\sqrt{n + 1} - \sqrt{n}) \frac{(\sqrt{n + 1} + \sqrt{n})}{\sqrt{n + 1} + \sqrt{n}}

= \frac{(n + 1) - n}{\sqrt{n + 1} + \sqrt{n}}

= \frac{1}{\sqrt{n + 1} + \sqrt{n}}

\lim_{n \to + \infty} \sqrt{n + 1} - \sqrt{n} = \lim_{n \to + \infty} \frac{1}{\sqrt{n + 1} + \sqrt{n}} = 0

8.5 Limites et inégalités.

Théorème 14

Soient

(u_{n})

(v_{n})

deux suites réelles.

Si les deux suites

(u_{n})

(v_{n})

convergent et que à partir d'un certain rang

n_{0} \in ℕ

, on a

\forall n ⩾ n_{0}, u_{n} ⩽ v_{n}

Alors

\lim_{n \to + \infty} u_{n} ⩽ \lim_{n \to + \infty} v_{n}

Théorème 15 (Théorème des Gendarmes)

Soient

(u_{n})

(v_{n})

(w_{n})

trois

suites réelles.

Si il existe un rang

n_{0} \in ℕ

tel que

\forall n ⩾ n_{0}

v_{n} ⩽ u_{n} ⩽ w_{n}

et si les suites

(v_{n})

(w_{n})

convergent vers la même limite

γ

, alors

(w_{n})

converge

et a pour limite

γ

Théorème 16 (Théorème de comparaison)

Soient

(u_{n})

(v_{n})

deux suites réelles.

On suppose qu'il existe un

n_{0} \in ℕ

tel que

\forall n ⩾ n_{0}

, on a

u_{n} ⩽ v_{n}

\lim_{n \to + \infty} u_{n} = + \infty

alors

\lim_{n \to + \infty} v_{n} = + \infty

\lim_{n \to + \infty} v_{n} = - \infty

alors

\lim_{n \to + \infty} u_{n} = - \infty

9. Suites monotones.

Théorème 17 (Théorème de la limite monotone)

1) Si la suite

(u_{n})

est croissante et majorée, alors la suite

(u_{n})

converge.

Si la suite

(u_{n})

est décrossante minorée, alors la suite

(u_{n})

converge.

2) Si la suite

(u_{n})

est croissante et non majorée, alors

\lim_{n \to + \infty} u_{n} = + \infty .

Si la suite

(u_{n})

est décroissante et non minjorée, alors

\lim_{n \to + \infty} u_{n} = - \infty .